Answer:
a) 0.74 μC b) q1 = 0.37 μC q₂ = 1.48 μC
Explanation:
Assuming that the spheres are small enough so both can be treated as point charges, the repulsive force between them must obey Coulomb's Law, as follows:
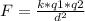
a) If the two charges are equal , q₁ = q₂ = q, then:
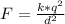
where k= 9*10⁹ N*m²/C², F= 0.220 N and d =0.15 m
Replacing in the above equation and solving for q, we have:
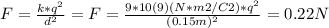
⇒
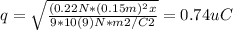
⇒ q₁ = q₂ = q = 0.74 μC
b) All the same considerations apply, the only difference is that for this case, q₁ = q and q₂ = 4*q.
The expression for the electrostatic force is now:
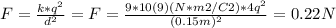
Solving for q;
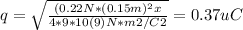
so, q₁= 0.37 μC ⇒ q₂ = 4*q₁ = 0.37 μC * 4 = 1.48 μC