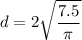Question

Calculate the diameter of a pipe that would carry 75.0 ft3/s of a liquid at an average velocity of 10.0 ft/s.

Answer 1

`d=3.1\ ft`

Step-by-step explanation:

Discharge (Hydrology)

The continuity equation states that for an incompressible fluid (like water) the discharge Q equals to the product of the stream's cross-sectional area (A) by its average velocity (v):

`Q=v.A`

The pipe described in the problem carries
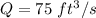`Q=75\ ft^3/s` of a liquid at an average velocity of v=10 ft/s. Let's compute the cross-sectional area by solving for A

`\displaystyle A=(Q)/(v)`

`\displaystyle A=(75)/(10)=7.5\ ft^2`

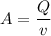
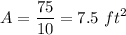
The pipe has a cross-section with the shape of a circle. Let's set d as the diameter of the circle, it's area is computed as

`\displaystyle A=(\pi d^2)/(4)`

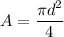
Solving for d

`\displaystyle d=2\sqrt{(A)/(\pi)}`

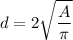
Replacing the value of A

`\displaystyle d=2\sqrt{(7.5)/(\pi)}`

`\boxed{d=3.1\ ft}`