Question

Given that ΔABC and ΔA'B'C' are similar right triangles that share the same slope, m, on the coordinate plane. Find the equation in the form y = mx that represents the line of the hypotenuses if ΔABC has a base defined by the coordinates of A = (3, 2) and B = (6, 2), and ΔA'B'C' has a height defined by the coordinates of B' = (9, 2) and C' = (9, 6).​

Answer 1

`y=(2)/(3)x`

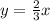
Explanation:

The similar triangles are drawn in the figure attached.

As shown in the figure, the smaller triangle ΔABC, and the larger triangle ΔA'B'C' share the same slope; therefore, the slope of the hypotenuse is the length of the triangle ΔA'B'C' divided by its base:

`m=(rise)/(run) =(height)/(base)= (4)/(6)=(2)/(3) \\\\ \boxed{m= (2)/(3)}`

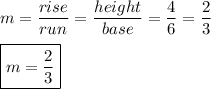
Therefore, the equation of the hypotenuse is

`\boxed{y=(2)/(3) x}`