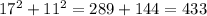Answer:
12 and 17
Explanation:
Let the two integers be m and n
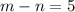

From the first equation,
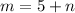
Substitute this in the second equation.
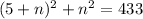
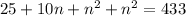
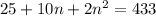
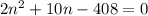
Divide both sides 2

Factorise to get
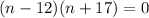
Therefore,
 or
or
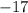
But
 is a positive integer. Therefore
is a positive integer. Therefore

From the first equation,
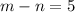
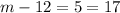
The two integers are 12 and 17.
Let's check
17 - 12 = 5