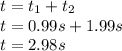Answer:
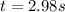
Step-by-step explanation:
First, we have to calculate the maximum height reached by the object. We use the equations of uniformly accelerated motion:

In order to calculate this, we have to know the time taken by the object to reach the maximum height:
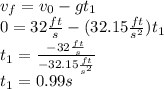
Now, we can calculate y:

Now, we calculate the time taken by the object in free fall:
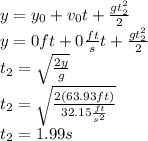
Finally, adding
 and
and
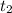 , we get the total time until the object impacts the ground:
, we get the total time until the object impacts the ground: