Question

Determine whether the given system has a unique solution, no solution, or infinitely many solutions.

Put the associated augmented matrix in reduced row-echelon form and find solutions, if any, in vector form. (If the system has infinitely many solutions, enter a general solution in terms of s. If the system has no solution, enter NO SOLUTION in any cell of the vector.)

−3x₁ + x₂ − 2x₃ = 8x₁ + 5x₂ − x₃ = 4 −x₁ + 11x₂− 4x₃ = 1

Answer 1

The system has no solution.

Explanation:

To find the solution to this system of linear equations

`\left\begin{array}{ccccc}-3x_1&+x_2&-2x_3&=&8&\\x_1&+5x_2&-x_3&=&4&\\-x_1&+11x_2&-4x_3&=&1&\end{array}\right`

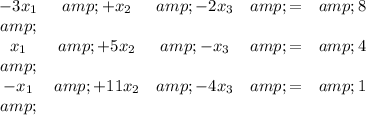
First, state the problem in matrix form, this means, extracting only the numbers, and putting them in a box.

`\left[ \begin{array}c -3 & 1 & -2 & 8 \\\\ 1 & 5 & -3 & 4 \\\\ -1 & 11 & -4 & 1 \end{array} \right]`

This is called an augmented matrix. The word “augmented” refers to the vertical line, which we draw to remind ourselves where the equals sign belong

Next, transform the augmented matrix to the reduced row echelon form with the help of Row Operations.

Row Operation 1: multiply the 1st row by -1/3

`\left[ \begin{array}ccc 1 & - (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 1 & 5 & -1 & 4 \\\\ -1 & 11 & -4 & 1 \end{array} \right]`

Row Operation 2: add -1 times the 1st row to the 2nd row

`\left[ \begin{array}ccc 1 & - (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & (16)/(3) & - (5)/(3) & (20)/(3) \\\\ -1 & 11 & -4 & 1 \end{array} \right]`

Row Operation 3: add 1 times the 1st row to the 3rd row

`\left[ \begin{array}ccc 1 & - (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & (16)/(3) & - (5)/(3) & (20)/(3) \\\\ 0 & (32)/(3) & - (10)/(3) & - (5)/(3) \end{array} \right]`

Row Operation 4: multiply the 2nd row by 3/16

`\left[ \begin{array}ccc 1 & - (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & 1 & - (5)/(16) & (5)/(4) \\\\ 0 & 0 & 0 & -15 \end{array} \right]`

Row Operation 5: add -32/3 times the 2nd row to the 3rd row

`\left[ \begin{array}c 1 &- (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & 1 & - (5)/(16) & (5)/(4) \\\\ 0 & 0 & 0 & -15 \end{array} \right]`

Row Operation 6: multiply the 3rd row by -1/15

`\left[ \begin{array}c 1 &- (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & 1 & - (5)/(16) & (5)/(4) \\\\ 0 & 0 & 0 & 1 \end{array} \right]`

Row Operation 7: add -5/4 times the 3rd row to the 2nd row

`\left[ \begin{array}ccc 1 &- (1)/(3) & (2)/(3) & - (8)/(3) \\\\ 0 & 1 & - (5)/(16) & 0 \\\\ 0 & 0 & 0 & 1 \end{array} \right]`

Row Operation 8: add 8/3 times the 3rd row to the 1st row

`\left[ \begin{array}ccc 1 &- (1)/(3) & (2)/(3) & 0 \\\\ 0 & 1 & - (5)/(16) & 0 \\\\ 0 & 0 & 0 & 1 \end{array} \right]`

Row Operation 9: add 1/3 times the 2nd row to the 1st row

`\left[ \begin{array}{cccc} 1 & 0 & (9)/(16) & 0 \\\\ 0 & 1 & - (5)/(16) & 0 \\\\ 0 & 0 & 0 & 1 \end{array} \right]`

The reduced row echelon form of the augmented matrix is

`\left[ \begin{array}{cccc} 1 & 0 & (9)/(16) & 0 \\\\ 0 & 1 & - (5)/(16) & 0 \\\\ 0 & 0 & 0 & 1 \end{array} \right]`

which corresponds to the system

`\left\begin{array}{ccccc}x_1&&+(9)/(16) x_3&=&0&\\&1x_2&-(5)/(16)x_3&=&0&\\&&0&=&1&\end{array}\right`

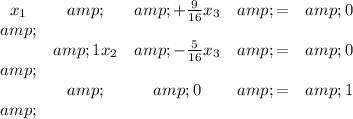
Equation 3 cannot be solved, therefore, the system has no solution.