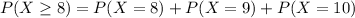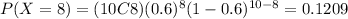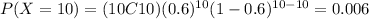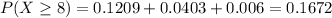Answer:
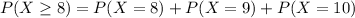
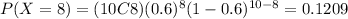

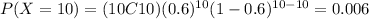
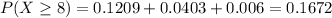
Explanation:
Previous concepts
The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".
Solution to the problem
Let X the random variable of interest (number of children that may have a blood level that may impair development), on this case we know that:

Since we select a sample of 10 and the probability of success for each trial is 0.6
The probability mass function for the Binomial distribution is given as:
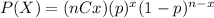
Where (nCx) means combinatory and it's given by this formula:
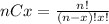
And we want to find this probability: