Question

A golf ball is hit with an initial velocity of 50 m/s at an angle of 45° above the horizontal. How far will the ball travel horizontally before it hits the ground?

Answer 1

255.1 m

Step-by-step explanation:

initial velocity pf projection, u = 50 m/s

angle of projection, θ = 45°

The horizontal range is given by

`R = (u^(2)Sin2\theta )/(g)`

`R = (50^(2)Sin90 )/(9.8)`

R = 255.1 m

Thus, the ball travel 255.1 m horizontally before hitting the ground.

Answer 2

The distance traveled by the ball before it hits the ground is 255.10 meters.

Step-by-step explanation:

Given that,

Initial velocity of the golf ball, u = 50 m/s

The angle of projection,
`\theta=45^(\circ)`

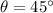
To find,

The distance traveled by the ball before it hits the ground.

Solution,

The distance covered by the projectile is called its horizontal range. It is given by the formula of range as :

`R=(v^2\ sin2\theta)/(g)`

`R=((50)^2\ sin2(45))/(9.8)`

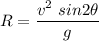
R = 255.10 meters

So, the distance traveled by the ball before it hits the ground is 255.10 meters.