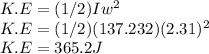Question

A horizontal 953 N merry-go-round of radius 1.68 m is started from rest by a constant horizontal force of 73.9 N applied tangentially to the merry-go-round. Find the kinetic energy of the merry-goround after 2.55 s. The acceleration of gravity is 9.8 m/s 2 . Assume the merry-go-round is a solid cylinder. Answer in units of J.

Answer 1

K.E=365.2 J

Step-by-step explanation:

Given data

Weight w =953 N

radius r=1.68 m

F=73.9 N

t=2.55 s

g=9.8 m/s²

To find

Kinetic Energy K.E

Solution

From the moment of inertia

`I=(1/2)MR^(2)\\ as \\W=mg\\So\\I=(1/2)(W/g)R^(2)\\I=(1/2)(953/9.8)(1.68)^(2)\\I=137.232kg.m^(2)`

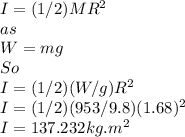
The angular acceleration is given as

`a=T/I\\a=(FR)/(I)\\ a=((73.9)(1.68))/(137.232)\\a=0.905rad/s^(2)`

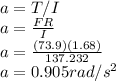
The angular velocity is given as

`w=at\\w=(0.905)(2.55)\\w=2.31rad/s`

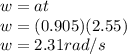
So the Kinetic Energy is given as

`K.E=(1/2)Iw^(2)\\ K.E=(1/2)(137.232)(2.31)^(2)\\ K.E=365.2J`