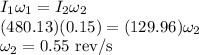Question

A merry-go-round rotates at the rate of 0.15 rev/s with an 97 kg man standing at a point 1.9 m from the axis of rotation. What is the new angular speed when the man walks to a point 0 m from the center? Consider the merry-go-round is a solid 72 kg cylinder of radius of 1.9 m. Answer in units of rad/s.

Answer 1

ω = 0.55 rev/s.

Step-by-step explanation:

Since there is no external torque, the angular momentum of the system is conserved. Therefore, the angular momentum when the man is at x = 1.9 m is equal to that of x = 0 m.

`L_1 = L_2\\I_1\omega_1 = I_2\omega_2`

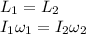
where I is the moment of inertia of the system. The system consist of the merry-go-round which is a solid cylinder and the man which can be regarded as a point object.

The total moment of inertia in the first case is

`I_1 = I_(cylinder) + I_(man) = (1)/(2)m_(cylinder)R_(cylinder)^2 + m_(man)d^2 = (1)/(2)(72)(1.9)^2 + (97)(1.9)^2 = 480.13`

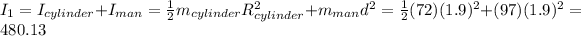
The moment of inertia in the second case is

`I_2 = (1)/(2)m_(cylinder)R_(cylinder)^2 + m_(man)(0) = (1)/(2)(72)(1.9)^2 = 129.96`

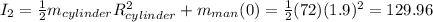
In the second case, the man has no contribution to the moment of inertia of the system, since he stands on the center.

Finally,

`I_1\omega_1 = I_2\omega_2\\(480.13)(0.15) = (129.96)\omega_2\\\omega_2 = 0.55~{\rm rev/s}`