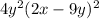Question

Expand the polynomial and simplify: (4xy− 1 8 y^2)^2

Answer 1

Answer:
`4y^(2)(2x-9y)^(2)`

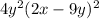
Explanation:

We have the following polynomial:

`(4xy-18y^(2))^(2)`

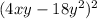
This is a polynomial of the form
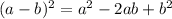`(a-b)^(2)=a^(2)-2ab+b^(2)`. Following this rule to expand it, we have:

`(4xy)^(2)-2(4xy)(18y^(2))+(18y^(2))^(2)`

`16x^(2)y^(2)-144xy^(3)+324y^(4)`

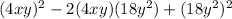
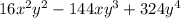
Applying common factor
`4y^(2)`:

`4y^(2)(4x^(2)-36xy+81y^(2))`

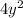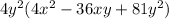
Note the polynomial inside the parenthesis is a perfect square trinomial, which can be factored to
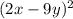`(2x-9y)^(2)`. Hence, the final simplification is:

`4y^(2)(2x-9y)^(2)`