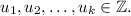Question

Let a1, a2, . . . , ak be integers with gcd(a1, a2, . . . , ak) = 1, i.e., the largest positive integer dividing all of a1, . . . , ak is 1. Prove that the equation a1u1 + a2u2 + · · · + akuk = 1

Answer 1

Solve by mathematical induction.

Explanation:

Let
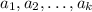`a_1,a_2, \ldots, a_k` be integers with
`GCD(a_1,a_2, \ldots ,a_k) = 1`.

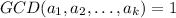We need to prove that

`a_1u_1 + a_2u_2 + \ldots + a_ku_k = 1`

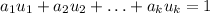
has a solution in integers
`u_1,u_2, \ldots, u_k \in \mathbb{Z}.`

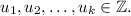
To do so, we will use mathematical induction.

The base case

Consider the case for
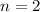`n=2`. Then,

`GCD(a_1,a_2) = 1`

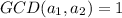
and we need to prove that

`a_1u_1 + a_2u_2 = 1`.

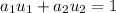Since the largest positive integer dividing
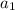`a_1` and
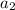`a_2` is 1, by the Euclidean algorithm, we have

`\left( \exist u_1, u_2 \in \mathbb{Z}\right) a_1u_1 + a_2u_2 = 1`

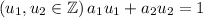
Therefore, the statement is true for
`n=2`.

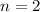The induction step

This step proves that if the property holds for one natural number
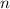`n`, then it holds for the next natural number
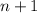`n+1`. Combined wit the base case, it will establish the property for
`\forall n \in \mathbb{N}.`

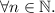
Now, suppose that the statement is true for
`n=k`.

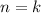This means that

`GCD(a_1, a_2, \ldots, a_k) = 1 \implies \left( \exists u_1, u_2, \ldots u_k \in \mathbb{Z}\right) a_1u_1 + a_2u_2 +\ldots+ a_ku_k = 1`

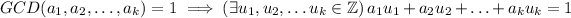
Let's check if the statement holds true for the next natural number, that is
`n= k+1`.

`GCD(a_1, a_2, \ldots, a_(k+1)) = 1 \implies GCD(a_1, a_2, \ldots, a_k) = 1 \: \wedge \: GCD(a_k, a_(k+1)) = 1`

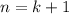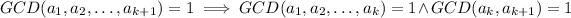
By the Euclidean algorithm, we have

`GCD(a_1, a_2, \ldots, a_(k)) = 1 \implies \left(\exists u_1,u_2, \ldots, u_k \in \mathbb{Z}\right)a_1u_1 + a_2u_2 + \ldots + a_ku_k = 1`

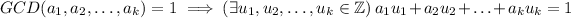
and

`GCD(a_k, a_(k+1)) = 1 \implies \left(\exists u_1,u_2, \in \mathbb{Z}\right)a_ku_k + a_(k+1)u_(k+1) = 1`

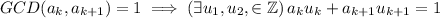
Now, multiply the obtained equations.

`(a_1u_1 + a_2u_2 + \ldots + a_ku_k)(a_ku_k + a_(k+1)u_(k+1)) = 1 \cdot 1`

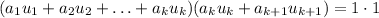
Removing parenthesis gives

`a_1u_1 \cdot a_ku_k + a_2u_2\cdot a_ku_k + \ldots + a_ku_k \cdot a_ku_k +\\a_1u_1 \cdot a_(k+1)u_(k+1) + a_2u_2\cdot a_(k+1)u_(k+1) + \ldots + a_ku_k \cdot a_(k+1)u_(k+1) =1`

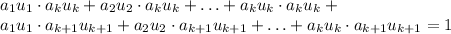
Now, collect up the terms by
`a_1, a_2, \ldots, a_(k+1)`.

`a_1\underbrace{(u_1 a_ku_k +u_1 \cdot a_(k+1)u_(k+1))}_{\in \mathbb{Z}}+ a_2\underbrace{(u_2 a_ku_k+ u_2 a_(k+1)u_(k+1) )}_{\in \mathbb{Z}} + \ldots + a_(k+1)\underbrace{(a_ku_k u_(k+1))}_{\in \mathbb{Z}} \\ =1`

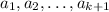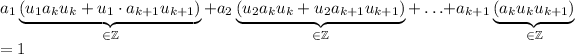
Now, denote

`u'_1 =u_1 a_ku_k +u_1 \cdot a_(k+1)u_(k+1),u'_2=u_2 a_ku_k+ u_2 a_(k+1)u_(k+1), \ldots, u'_(k+1) =a_ku_ku_(k+1)`

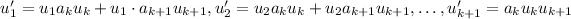
Therefore,

`\left(\exists u'_1,u'_2, \ldots, u'_(k+1) \in \mathbb{Z}\right)a_1u'_1 + a_2u'_2 + \ldots + a_(k+1)u'_(k+1) = 1`

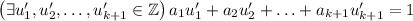
Hence, the equation

`a_1u_1 + a_2u_2 + \ldots + a_ku_k = 1`

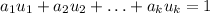
has a solution in integers
`u_1,u_2, \ldots, u_k \in \mathbb{Z}.`