Question

The center on a target has a diameter of 5 inches. The whole target has a diameter of 25 inches. Complete the explanation for what part of the whole target is the center.

Answer 1

The center is
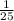`(1)/(25)` of the whole target.

Explanation:

Given:

Diameter of the center = 5 inches

Diameter of the whole target = 25 inches

We need to find the part of the center to the whole target.

Solution,

Firstly we will find out the areas of center and whole target.

For center;

Diameter = 5 in

Radius of circle is equal to half of the diameter.

radius =
`(diameter)/(2)=(5)/(2)=2.5\ in`

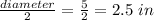
Now we know that the area of circle is equal to π times square of the radius.

framing in equation form, we get;

Area =
`\pi *{2.5}^2`

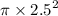
For whole target;

Diameter = 25 in

Radius of circle is equal to half of the diameter.

radius =
`(diameter)/(2)=(25)/(2)=12.5\ in`

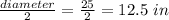
Now we know that the area of circle is equal to π times square of the radius.

framing in equation form, we get;

Area =
`\pi *12.5^2`

Now to find the part of the center to the whole target we will divide Area of center with Area of the target.

framing in equation form we get;

the part of the center to the whole target =
`(\pi *2.5^2)/(\pi *12.5^2)= (6.25)/(156.25) = (1)/(25)`

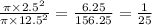
Hence the center is
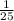`(1)/(25)` of the whole target.