Question

A group of 25 particles have the following speeds:

two have speed 11 m/s, seven have 17 m/s, four have 19 m/s, three have 27 m/s, six have 32 m/s, one has 33 m/s, and two have 40 m/s.

(a) Determine the average speed.
(b) Determine the RMS speed.
(c) Determine the most probable speed.

Answer 1

Part a: The average speed is 24.12 m/s

Part b: The rms speed is 25.55 m/s

Part c: The most probable speed is 17 m/s.

Step-by-step explanation:

Part a

Average Speed

Average speed is given as

`v_(avg)=(\sum)/(n)`

`v_(avg)=((2 * 11) +(7 * 17)+(4 * 19)+(3 * 27) +(6 * 32) +(1 * 33)+(2 * 40) )/(25)\\v_(avg)=(22+119+76+81+192+33+80)/(25)\\v_(avg)=(603)/(25)\\v_(avg)=24.12 m/s`

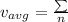
So the average speed is 24.12 m/s

Part b

RMS Speed

`v_(rms)=(\sum v^2)/(n)`

`v_(rms)=\sqrt{((2 * 11^2) +(7 * 17^2)+(4 * 19^2)+(3 * 27^2) +(6 * 32^2) +(1 * 33^2)+(2 * 40^2) )/(25)} \\v_(rms)=\sqrt{(242+2023+1444+2187+6144+1089+3200)/(25)}\\\\v_(rms)=\sqrt{(16329)/(25)}\\v_(rms)=√(653.16)\\v_(rms)=25.55 m/s`

So the rms speed is 25.55 m/s

Part c

Most Probable Speed

As 7 particles have speed of 17 m/s i.e. 7 is the highest frequency so 17 m/s is the most probable speed.