Question

Suppose that a sample of size 100 is to be drawn from a population with standard deviation L0. a. What is the probability that the sample mean will be within 2 of the value of p?

Answer 1

The probability that the sample mean will lie within 2 values of μ is 0.9544.

Explanation:

Here

• the sample size is given as 100
• the standard deviation is 10

The probability that the sample mean lies with 2 of the value of μ is given as

`P(| \bar{X}-\mu|<2)\\P(-2<\bar{X}-\mu<2)\\`

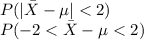
Here converting the values in z form gives

`P(-2<\bar{X}-\mu<2)\\P(\frac{-2}{\frac{\sigma} {√(n)}}<\frac{\bar{X}-\mu}{\frac{\sigma} {√(n)}}<\frac{2}{\frac{\sigma} {√(n)}})`

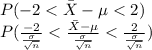
Substituting values

`P(-2<\bar{X}-\mu<2)\\P(\frac{-2}{\frac{10} {√(100)}}<z<\frac{2}{\frac{10} {√(100)}})\\P(-2<z<2)=P(z<2)-P(z<-2)`

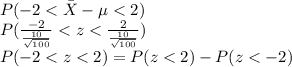
From z table

`P(z\leq 2)=0.9772\\P(z\leq -2)=0.0228\\P(-2\leq z\leq 2)=P(z\leq 2)-P(z\leq -2)\\P(-2\leq z\leq 2)=0.9772-0.0228\\P(-2\leq z\leq 2)=0.9544\\`

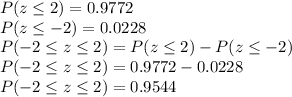
So the probability that the sample mean will lie within 2 values of μ is 0.9544.