Question

A soccer ball is kicked from the ground with an initial speed of 20.5 m/s at an upward angle of 45°. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to catch the ball just before it hits the ground?

Answer 1

S = 4.08 m/s

Step-by-step explanation:

given,

initial speed, v = 20.5 m/s

angle made with horizontal, θ = 45°

Distance of player = 55 m

Average speed of the player to catch the ball = ?

vertical velocity of the ball =

v_y = v sin θ = 20.5 x sin 45° = 14.5 m/s

horizontal velocity of the ball

v_x = v cos θ = 20.5 x cos 45° = 14.5 m/s

time taken by the ball to reach at the highest point

v = u + g t

v = V_y - g t

0 = 14.5 - 9.8 x t

t = 1.48 s

total time of flight = 2 t = 1.48 x 2 = 2.96 s

Horizontal distance travel by the ball

s = vₓ x t

s = 14.5 x 2.96

s = 42.96 m

distance player has to run

D = 55 - 42.96 = 12.08 m

Average speed of the player

`S = (D)/(t)`

`S = (12.08)/(2.96)`

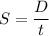
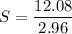
S = 4.08 m/s

Speed of the player is equal to 4.08 m/s