Answer:
9.2m/s
Step-by-step explanation:
We are given that
Radial velocity=

Angular velocity=
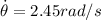
Displacement=r=3.58 m
We have to find the magnitude of velocity of particle in m/s.
The magnitude of velocity of particle in polar coordinates is given by

Using the formula
The magnitude of velocity of particle
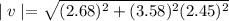

Hence, the magnitude of velocity of particle=9.2m/s