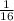Answer:
1/16
Explanation:
Place x=0 and you can see
 indefinitness. So you can apply the l'hosptial rule. Its basic you should
indefinitness. So you can apply the l'hosptial rule. Its basic you should
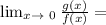
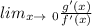 so apply the derivative
so apply the derivative
![\frac{(1)/(x-4) +\frac{1}{\sqrt[4]{(1-x})^3 } }{2x}](https://img.qammunity.org/2023/formulas/mathematics/college/agpvlbisj7aw8qrdxlbfy2uzu7hrh1ndyh.png) and replace the x=0 and you'll see same answer
and replace the x=0 and you'll see same answer
 re-apply the l'hospital rule and answer
re-apply the l'hospital rule and answer
![\frac{(-1)/((x-4)^2) + \frac{3}{16\sqrt[4]{(1-x)^7} } }{2}](https://img.qammunity.org/2023/formulas/mathematics/college/wl1smatnxn3d1pfzjcx9r9evgc9o4b4nml.png) and replace the 0 you can see the answer
and replace the 0 you can see the answer