Answer:

8 calculators at most.
Explanation:
Let x represent number of calculators.
We have been given that each calculator costs $15. So the cost of x calculators would be
 dollars.
dollars.
Since the order must be less than $125 in order to not go over budget, so cost of x calculators should be less than or equal to 125. We can represent this information in an inequality as:

Therefore, our required inequality would be
 .
.
Let us divide both sides of inequality by 15 as:
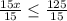
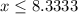
Since we cannot order 0.33 of a calculator, therefore, the math club can order 8 calculators at most.