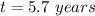Answer:
5.7 years
Explanation:
we know that
The compound interest formula is equal to
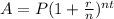
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
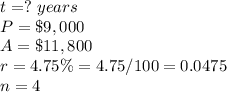
substitute in the formula above

Solve for t
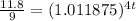
Applying property of exponents
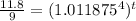
Applying log both sides
![log((11.8)/(9))=log[(1.011875^(4))^(t)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wacp23lqhqozml6o0sr5alhj0deaux8hg3.png)
![log((11.8)/(9))=(t)log[(1.011875^(4))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/typ6kcg0f3gkm9t8583ifsfeqvaew1fkxu.png)
![t=log((11.8)/(9))/log[(1.011875^(4))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/a0km0c5mst612b9t89sqfp7qi8bhjq4z3x.png)