Question

A rectangular parking lot has an area of 315 square yards. The width of the parking lot is 5 yards longer than the length of the parking lot. What are the dimensions of the parking lot?

Answer 1

Dimension of parking lot is approximately 15.425 × 20.425 yards.

Explanation:

Given:

Area of the parking lot =
`315 \ yd^2`

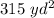
Let the length of the parking lot be
`'l'`

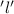
Also Given:

The width of the parking lot is 5 yards longer than the length of the parking lot.

so we can say that;

width of the parking lot,
`w=5+l`

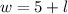
We need to find the dimension of parking lot.

Solution:

Now we can say that;

Area of rectangle is equal to length times width.

framing in equation form we get;

`lw=315`

Now substituting the value of w in above equation we get;

`l(l+5)=315\\\\l^2+5l=315\\\\l^2+5l-315=0`

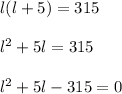
Now we will find the roots using quadratic equation.

`ax^2+bx+c =0`

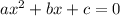
a = 1

b=5

c=-315

Formula for quadratic equation is;

`l =(-b\±√(b^2-4ac))/(2a)`

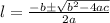
First we will find;

`√(b^2-4ac) = √(5^2-4*1*-315) =√(25+1260)=√(1285) \approx35.85`

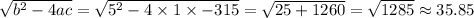
Now we will substitute the value we get;

`l =(-5\±35.85)/(2*1)= (-5\±35.85)/(2)`

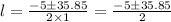
Now we will find 2 roots we get;

`l= (-5+35.85)/(2)= (30.85)/(2)\approx15.425\\\\OR\\\\l =(-5-35.85)/(2)= (-40.85)/(2) \approx -20.425`

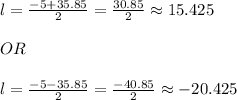
Now we get 2 values of length one is positive and other is negative.

But length of parking lot cannot be negative hence we will discard the negative value.

Hence the length of the parking lot = 15.425 yards

Width of the rectangular parking lot =
`l+5=15.425+5 =20.425`

Hence we can say that dimension of parking lot is approximately 15.425 × 20.425 yards.