Answer: 539.4 N
Step-by-step explanation:
Let's begin by explaining that Coulomb's Law establishes the following:
"The electrostatic force
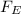 between two point charges
between two point charges
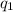 and
and
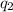 is proportional to the product of the charges and inversely proportional to the square of the distance
is proportional to the product of the charges and inversely proportional to the square of the distance
 that separates them, and has the direction of the line that joins them"
that separates them, and has the direction of the line that joins them"
What is written above is expressed mathematically as follows:
 (1)
(1)
Where:
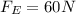 is the electrostatic force
is the electrostatic force
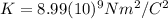 is the Coulomb's constant
is the Coulomb's constant
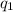 and
and
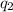 are the electric charges
are the electric charges
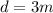 is the separation distance between the charges
is the separation distance between the charges
Then:
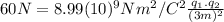 (2)
(2)
Isolating
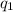 and
and
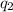 :
:
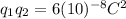 (3)
(3)
Now, if we keep the same charges but we decrease the distance to
 , (1) is rewritten as:
, (1) is rewritten as:
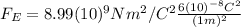 (4)
(4)
Then, the new electrostatic force will be:
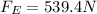 (5) As we can see, the electrostatic force is increased when we decrease the distance between the charges.
(5) As we can see, the electrostatic force is increased when we decrease the distance between the charges.