Question

An injection-molded part is likely to be obtained from any 1 of 10 cavities on a mold. Round your answers to three decimal places (e.g. 98.765).

(a) What is the probability that a part is from cavity 1, 2 or 3?
(b) What is the probability that a part is neither from cavity 3 nor 4?

Answer 1

a) 0.3

b) 0.8

Explanation:

We are given the following in the question:

An injection-molded part is likely to be obtained from any 1 of 10 cavities on a mold.

Thus, the sample space could be written as:

`S = \{C_1,C_2,C_3,C_4,C_5,C_6,C_7,C_8,C_9,C_(10)\}`

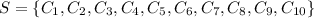
where C are the cavities on mold.

Each cavity of equal likelihood.

`\text{Probability} = \displaystyle\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}`

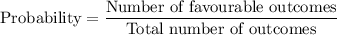
a) probability that a part is from cavity 1, 2 or 3

`P(C_1,C_2~or~ C_3) = (3)/(10) = 0.3`

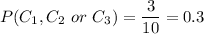
0.3 is the probability that a part is from cavity 1, 2 or 3.

b) probability that a part is neither from cavity 3 nor 4

`P(C'_3\cup C'_4)\\=1 - P(C_3\cup C_4)\\=1 - (2)/(10)\\\\=1 - (1)/(5) = (4)/(5) = 0.8`

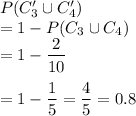
0.8 is the probability that a part is neither from cavity 4 or cavity 4.