Question

A dog sits 1.70 m from the center of a merrygo-round with an angular speed of 1.27 rad/s. If the magnitude of the force that maintains the dog’s circular motion is 40.3 N, what is the dog’s mass? Answer in units of kg.

Answer 1

Answer : The mass of dog is, 14.7 kg

Solution :

Formula used for centripetal force is,

`F_c=(m* v^2)/(r)`

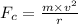
As we know that,

`\omega =(v)/(r)`

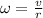
or,

`\omega * r=v`

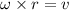
So,

`F_c=(m* (\omega * r)^2)/(r)`

`F_c=m* (\omega)^2* r`

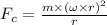
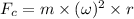
where,

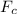`F_c` = centripetal force = 40.3 N

m = mass of dog = ?

r = radius of path = 1.70 m

v = velocity or speed

`\omega` = angular speed = 1.27 rad/s

Now put all the given values in the above formula, we get the centripetal force.

`F_c=m* (\omega)^2* r`

`40.3=m* (1.27)^2* (1.70)`

`m=14.7kg`

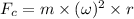
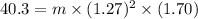
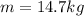
Thus, the mass of dog is, 14.7 kg