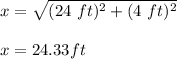Question

Andrew needs a ladder to hang hoilday lights. His house is 24ft tall and he has a flower bef that extends 4 ft out from the side of the house. How long of a ladder will he need to reach the top and be out of the flower bed

Answer 1

Answer:
`24.33\ ft`

Explanation:

You need to draw a Right triangle as the one attached, where "x" is the lenght of a ladder Andrew will need to reach the top and be out of the flower bed.

You must apply the Pythagorean Theorem. This is:

`a^2=b^2+c^2`

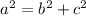
Where "a" is the hypotenuse and "b" and "c" are the legs of the Right triangle.

If you solve for "a", you get:

`a=√(b^2+c^2)`

In this case, you can identify in the figure that:

`a=x\\\\b=24\ ft\\\\c=4\ ft`

Therefore, knowing those values, you can substitute them into
`a=√(b^2+c^2)` and then you must evaluate, in order to find the value of "x".

This is:

`x=√((24\ ft)^2+(4\ ft)^2)\\\\x=24.33 ft`