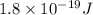Question

What is the energy (in J) of a photon that is ejected from a hydrogen atom when an electron relaxes from the 6th to the 3rd energy level ?

Answer 1

Answer:
`1.8* 10^(-19)J`

Step-by-step explanation:

Using Rydberg's Equation for hydrogen atom:

`(1)/(\lambda)=R_H\left((1)/(n_i^2)-(1)/(n_f^2) \right )`

Where,

`\lambda` = Wavelength of radiation

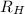`R_H` = Rydberg's Constant

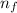`n_f` = Higher energy level

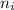`n_i`= Lower energy level

We have:

`n_f=6, n_i=3`

`R_H=1.09* 10^7 m^(-1)`

`(1)/(\lambda)=1.09* 10^7 m^(-1)* \left((1)/(3^2)-(1)/(6^2) \right )`

`(1)/(\lambda)=1.09* 10^7 m^(-1)* (3)/(36)`

`(1)/(\lambda)=0.0908* 10^(7)m^(-1)`

`\lambda=11.0* 10^(-7) m`

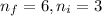
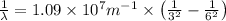
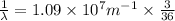
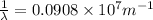
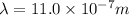
The relation between energy and wavelength of light is given by Planck's equation, which is:

`E=(hc)/(\lambda)`

where,

E = energy of the light

h = Planck's constant

c = speed of light

`\lambda` = wavelength of light

`E=(6.6* 10^(-34)* 3* 10^8)/(11.0* 10^(-7)m)`

`E=1.8* 10^(-19)J`

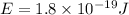
Thus energy of a photon that is ejected from a hydrogen atom when an electron relaxes from the 6th to the 3rd energy level is
`1.8* 10^(-19)J}`