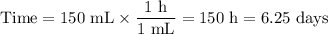Question

Freeze-drying is a process used to preserve food. If strawberries are to be freeze-dried, then they would be frozen to -80.00 °C

and subjected to a vacuum of 1.00 mtorr. As the water is removed, it is frozen to a cold surface in the freeze-drier. If 150 mL of
water has to be removed from a batch of strawberries, how much energy would be required?
At any given time, how much water is in the atmosphere if the volume of the freeze-drier is 5 liters?


If it takes one hour to remove one mL of water, how long will it take to freeze-dry the strawberries?

Answer 1

1. 389 kJ; 2. 7.5 µg; 3. 6.25 days

Step-by-step explanation:

1. Energy required

The water is converted directly from a solid to a gas (sublimation).

They don't give us the enthalpy of sublimation, but

`\Delta_{\text{sub}}H = \Delta_{\text{fus}}H + \Delta_{\text{vap}}H = 6.01 + 40.68 = 46.69 \text{ kJ}\cdot\text{mol}^(-1)`

The equation for the process is then

Mᵣ: 18.02

46.69 kJ + H₂O(s) ⟶ H₂O(g)

m/g: 150

(a) Moles of water

`\text{Moles} = \text{150 g} * \frac{\text{1 mol}}{\text{18.02 g}} = \text{8.324 mol}`

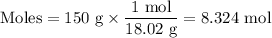
(b) Heat removed

46.69 kJ will remove 1 mol of ice.

`\text{Heat removed} = \text{8.234 mol} * \frac{\text{46.69 kJ}}{\text{1 mol}} = \textbf{389 kJ}\\\text{It takes $\large \boxed{\textbf{389 kJ}}$ to remove 150 g of ice}`

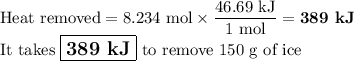
2. Mass of water vapour in the freezer

For this calculation, we can use the Ideal Gas Law — pV = nRT

(a) Moles of water

Data:

`p = 1.00 * 10^(-3)\text{ torr } * \frac{\text{1 atm}}{\text{760 torr}} = 1.316 * 10^(-6)\text{ atm}`

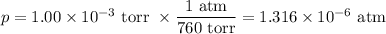
V = 5 L

T = (-80 + 273.15) K = 193.15 K

Calculation:

`\begin{array}{rcl}pV & = & nRT\\1.316 * 10^(-6)\text{ atm} * \text{5 L} & = & n * 0.08206 \text{ L}\cdot\text{atm}\cdot\text{K}^(-1)\text{mol}^(-1) * \text{193.15 K }\\6.6 * 10^(-6) & = & 15.85n\text{ mol}^(-1) \\n & = & \frac{6.6 * 10^(-6)}{15.85\text{ mol}^(-1)}\\\\& = & 4.2 * 10^(-7) \text{ mol}\\\end{array}`

(b) Mass of water

`\text{Mass} = 4.2 * 10^(-7) \text{ mol} * \frac{\text{18.02 g}}{\text{1 mol}} = 7.5 * 10^(-6)\text{ g} = 7.5 \, \mu \text{g}\\\\\text{At any given time, there are $\large \boxed{\textbf{7.5 $\mu$g}}$ of water vapour in the freezer.}`

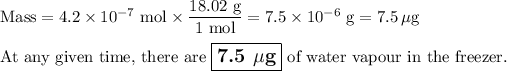
3. Time for removal

You must remove 150 mL of water.

It takes 1 h to remove 1 mL of water.

`\text{Time} = \text{150 mL} * \frac{\text{1 h}}{\text{1 mL}} = \text{150 h} = \text{6.25 days}`