Question

Consider the first order differential equation a) Is this a linear system? In other words, show whether superposition and homogeneity are satisfied. b) What is the solution of this differential equation? Give the most general expression.

Answer 1

To determine if a differential equation is linear, we need to check if it satisfies superposition and homogeneity. The most general solution to a first order linear differential equation can be found using an integrating factor.

Step-by-step explanation:

No specific differential equation was mentioned in the question. However, given the context, I will assume a general first order differential equation in the form:

dy/dx + P(x)y = Q(x)

a) To determine if it is a linear system, we need to check if it satisfies superposition and homogeneity. A differential equation is linear if it satisfies both properties.
For superposition, if y1 and y2 are solutions to the differential equation, then c1y1 + c2y2 is also a solution, where c1 and c2 are constants. To check superposition, substitute the values of y1 and y2 into the differential equation and verify if c1y1 + c2y2 also satisfies the equation.
For homogeneity, check if c * y satisfies the equation, where c is a constant and y is a solution. Substitute the value of c * y into the differential equation and verify if it satisfies the equation.

b) The most general solution to a first order linear differential equation can be found using an integrating factor. Multiply the entire equation by the integrating factor e^(integral of P(x)dx). Then solve the resulting equation as a separable differential equation and integrate to find the general solution.

I hope this helps! Let me know if you have any further questions.

Answer 2

Part a: The equation is a linear first order differential equation as superposition and homogeneity is satisfied.

Part b: The solution of the differential equation is
`y(t)=(u(t)-e^(-kt) u(t))/(k)`

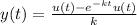
Step-by-step explanation:

Part a:

Let us suppose the differential equation is given as

`(d)/(dy) y(t) +k y(t)=u(t)`

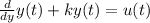
For a solution, it is given as

`(d)/(dy) y_1(t) +k y_1(t)=u_1(t)`

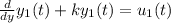
For another solution it is given as

`(d)/(dy) y_2(t) +k y_2(t)=u_2(t)`

Adding these two solution gives

`(d)/(dy) y_1(t) +k y_1(t)=u_1(t) \\+ \\(d)/(dy) y_2(t) +k y_2(t)=u_2(t)\\\\(d)/(dy) (y_1(t)+y_2(t)) +k (y_1(t)+y_2(t))=(u_1(t)+u_2(t))`

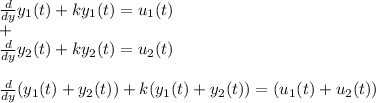
Which is also the solution of the equation and thus as superposition (additivity) and homogeneity is satisfied, so the equation is a linear first order differential equation.

Part b

`(d)/(dy) y(t) +k y(t)=u(t)`

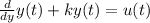
So taking Laplace on both sides

`s Y(s)+kY(s)=(1)/(s)`

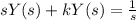
Here

`u(t)=(1)/(s)`

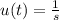
Rearranging the equation gives

`Y(s)=(1)/(k(s+k))\\Y(s)=(1)/(k)[(1)/(s)-(1)/(s+k)]\\`

Taking inverse Laplace gives

`y(t)=(u(t)-e^(-kt) u(t))/(k)`

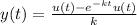
This is the solution of the differential equation.