Answer: See below
Explanation:
The function of the seat’s height from the ground level is given as,
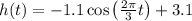
Here, t denotes the time.
(a) The height will be maximum or minimum when the derivative of the function of height is equal to zero.

The height of the seat at time t = 0 s can be determined as,
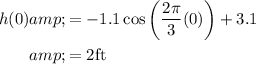
Therefore, the maximum height of the swing is 4.2 ft and the minimum height of the swing is 2 ft.
(b) The height of the swing is given as,
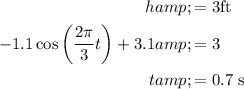
Therefore, the first time after t = 0 s that the swing’s height of 3 ft is 0.7 s.
(c) The height of the swing is given as,

Therefore, the second time after t = 0 s that the swing’s height of 3 ft is 3.7 s.