Question

Determine whether each of the following is true or false (note: the statement is true if it is always true, otherwise it is false). If you say it is true than give a proof, while if you say it is false then give a counterexample, i.e., a particular case where it fails.

(a) A − B = A ∪ B

(b) Pr (A ∪ B) ≤ Pr (A) + Pr (B)

(c) Pr (A|B) ≥ Pr (A) if B ⊃ A

(d) If A1 . . . , An are mutually exclusive, then Pr (B) = Pn i=1 Pr (B|Ai) Pr (Ai)

Answer 1

Explanation:

We are given four statements and we must check whether true or false

a) A − B = A ∪ B

False

Eg: A={1,2} B = {2,3}

A-B = {1}

AUB ={1,2,3} not equal

(b) Pr (A ∪ B) ≤ Pr (A) + Pr (B)

True because

Pr (A ∪ B)=Pr (A) + Pr (B) -P(AB), where P(AB)≥0

(c) Pr (A|B) ≥ Pr (A) if B ⊃ A

If A is a subset of B, we have P(AB) = P(A)

So P(A/B ) = P(A)/P(B) ≥P(A) since P(B) is always less than or equal to 1

(d) If A1 . . . , An are mutually exclusive, then Pr (B) = Pn i=1 Pr (B|Ai) Pr (Ai)

P(B) =
`\Sigma P(A_i B)`

=
`\Sigma _1^n P(A_i) P(B/A_i)`

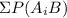
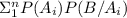
so true