Answer:
The true anomaly q will be such that the q=
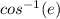 where e is the eccentricity of the ellipse.
where e is the eccentricity of the ellipse.
Step-by-step explanation:
For ellipse velocity components and velocity is given as
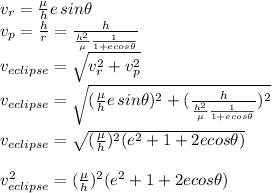
For similar radius velocity of circle is given as
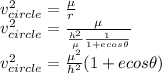
Now as per the condition
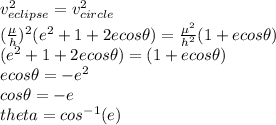
So the true anomaly q will be such that the q=
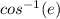 where e is the eccentricity of the ellipse.
where e is the eccentricity of the ellipse.