Question

Ocean waves pass through two small openings, 20.0 m apart, in a breakwater. You're in a boat 70.0 m from the breakwater and initially midway between the openings, but the water is pretty rough. You row 33.0 m parallel to the breakwater and, for the second time, find yourself in relatively calm water. What is the wavelength of the ocean waves ?

Answer 1

λ = 5.65m

Step-by-step explanation:

The Path Difference Condition is given as:

δ=
`(m+(1)/(2))(lamda)/(n)` ;

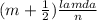where lamda is represent by the symbol (λ) and is the wavelength we are meant to calculate.

m = no of openings which is 2

∴δ=
`(3*lamda)/(2)`

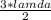
n is the index of refraction of the medium in which the wave is traveling

To find δ we have;

δ=
`\sqrt{70^2+(33+(20)/(2))^2 }-\sqrt{70^2+(33-(20)/(2))^2 }`

δ=
`\sqrt{4900+((66+20)/(2))^2}-\sqrt{4900+((66-20)/(2))^2}`

δ=
`\sqrt{4900+((86)/(2))^2 }-\sqrt{4900+((46)/(2))^2 }`

δ=
`√(4900+43^2)-√(4900+23^2)`

δ=
`√(4900+1849)-√(4900+529)`

δ=
`√(6749)-√(5429)`

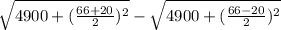
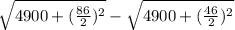
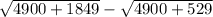
δ= 82.15 -73.68

δ= 8.47

Again remember; to calculate the wavelength of the ocean waves; we have:

δ=
`(3*lamda)/(2)`

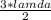
δ= 8.47

8.47 =
`(3*lamda)/(2)`

λ =
`(8.47*2)/(3)`

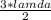
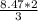
λ = 5.65m