Answer:
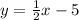
Step-by-step explanation:
Slope-intercept form: y = mx + b
m = slope

To find slope, we use points on the line.
Here, I will be suing (-6, -8) and (8, -1)
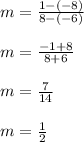

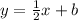
Now, we use either of our points (-6, -8) OR (8, 1) to find b.
I will be using (8, -1):
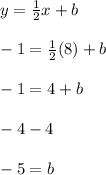

Check your answer manually: (-6, -8)
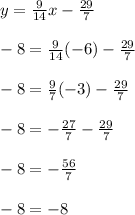
This statement is correct.
*You can also view the attached graph to verify the answer, meaning that those two points should lie on the same line.*
Hope this helps!