Question

Given the data points, (x, y) of a linear function: (2, 11), (4, 10), (6, 9), (12, 6), what is the function? What is the slope? What is the intercept?

Answer 1

The function is
`y~=~12 ~-~ 0.5 \cdot x`.

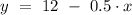The slope is
`m=-0.5`.

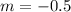The y-intercept is
`b=12`.

Explanation:

Our aim is to calculate the values m (slope) and b (y-intercept) in the equation of a line :

`y=mx+b`

We have the following data:

`\begin{array}ccccx&2&4&6&12\\y&11&10&9&6\end{array}`

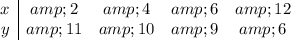
To find the line of best fit for the points given, you must:

Step 1: Find
`X\cdot Y`and
`X\cdot X` as it was done in the table below.

Step 2: Find the sum of every column:

`\sum{X} = 24 ~,~ \sum{Y} = 36 ~,~ \sum{X \cdot Y} = 188 ~,~ \sum{X^2} = 200`

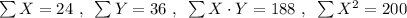
Step 3: Use the following equations to find b and m:

`\begin{aligned} b &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = ( 36 \cdot 200 - 24 \cdot 188)/( 4 \cdot 200 - 24^2) \approx 12 \\ \\m &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = ( 4 \cdot 188 - 24 \cdot 36 )/( 4 \cdot 200 - \left( 24 \right)^2) \approx -0.5\end{aligned}`

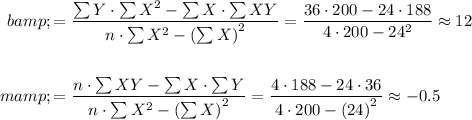
Step 4: Assemble the equation of a line

`\begin{aligned} y~&=~b ~+~ m \cdot x \\y~&=~12 ~-~ 0.5 \cdot x\end{aligned}`

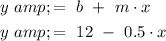
The graph of the regression line is: