Answer:
![\displaystyle \sqrt[14]{x^3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/lat5gswe9emx7ptgzkvgkbuiw5h4hfu881.png)
Explanation:
Radical As A Fractional Exponent
We can write a radical as a fractional exponent. The power to which the base is raised is the numerator and the root is the denominator. For example, the radical
![\sqrt[5]{x^3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ckflj42m2ypny663gvhcpy77cppu1h7tgu.png)
is equivalent to
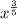
A) The simplification shown in the image is wrong because the student subtracted the roots of the radicals separated from the subtraction of the powers.
B) The correct procedure is
* Express both radicals as fractional exponents
* Subtract both exponents
* Simplify the resultant fraction
* Return the fractional exponent to radical form
In our case, the correct procedure is
![\displaystyle \frac{\sqrt[7]{x^5}}{\sqrt[4]{x^2}}=\frac{x^{(5)/(7)}}{x^{(2)/(4)}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/acnsgrnx8mu85wmm3bt4lmf5rujuq6s3a8.png)
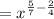

![\displaystyle \boxed{ \sqrt[14]{x^3}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/tglitekk0np70dmtdm3vsjwk7ocpk943i4.png)