Question

The sum of four consecutive terms of an arithmetic progression is 32 and the ratio of product of the first and the last term to the product of two middle terms is 7:15.

Find the numbers. ​

Answer 1

The four consecutive terms are 2,6,10,14.

Step-by-step explanation:

Let the four consecutive terms of an arithmetic progression be (a - 3d), (a - d),(a + d), (a + 3d)

It is given that the sum of four consecutive terms is 32.

Thus, adding all the four consecutive terms, we have,

`\begin{array}{r}{a-3 d+a-d+a+d+a+3 d=32} \\{4 a=32} \\{a=8}\end{array}`

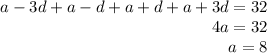
Thus, the value of a is 8.

It is also given that the ratio of the product of first and last term to the product of the two middle terms is 7:15. Thud, we have,

`((a-3d)(a+3d))/((a-d)(a+d)) =(7)/(15)`

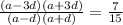
Simplifying the terms, we have,

`$\begin{aligned} (a^(2)-9 d^(2))/(a^(2)-d^(2)) &=(7)/(15) \\ 15\left(a^(2)-9 d^(2)\right) &=7\left(a^(2)-d^(2)\right) \\ 15 a^(2)-135 d^(2) &=7 a^(2)-7 d^(2) \\ 8 a^(2) &=128 d^(2) \end{aligned}$`

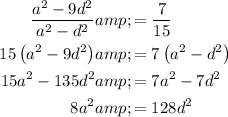
Now, substituting a = 8, we have,

`$\begin{aligned} 8(64) &=128 d^(2) \\ 512 &=128 d^(2) \\ 4 &=d^(2) \\ 2 &=d \end{aligned}$`

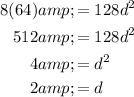
Thus, the value of d is 2.

Now, we shall substitute the value of a and d in the terms (a - 3d), (a - d),(a + d), (a + 3d), we get, the four consecutive terms.

Thus, the four consecutive terms are 2,6,10,14.