Question

A basketball player shoots a basketball with an initial velocity of 15 ft/sec. The ball is released from an initial height of 6.5 feet. PLEASE HELP

Answer 1

1.
`h(t)=-16t^2+15t+6.5`

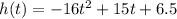
2. The ball hits the ground at t = 1.26 seconds

3. The basketball reaches its maximum height at t=0.47 seconds

4. The maximum height of the ball is 3.52 feet

Explanation:

Function Modeling

Reality can sometimes be modeled by mathematics. Functions are a great tool to explain the behavior of the measured magnitudes, it can also be used to predict future values and help to make decisions.

We are given a function to model the height (in feet) of a basketball once it's shot from the player. The function is

`h(t)=-16t^2+v_ot+h_o`

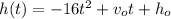
where t is the time in seconds,
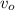`v_o` the initial speed and
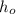`h_o` the initial height. We are also given the values

Part 1

`v_o=15\ ft/s,\ h_o=6.5\ ft`

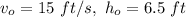
The complete model is

`h(t)=-16t^2+15t+6.5`

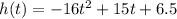
Part 2

To find the time the basketball hits the ground, we must set its height to zero:

`-16t^2+15t+6.5=0`

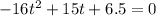
To solve this quadratic equation, we'll use the solver formula

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

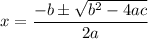
where a = -16, b = 15, c = 6.5

`\displaystyle t=(-15\pm √(15^2-4* (-16)* 6.5))/(2(-16))`

`\displaystyle t=(-15\pm 25.32)/(-32)`

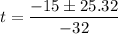
This produces two solutions:

`t=-0.322\ sec,\ t=1.26\ sec`

We discard the negative solution because time cannot be negative, thus the ball hits the ground at t = 1.26 seconds

Part 3

A quadratic function of the form

`at^2+bt+c`

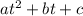
has its extrema value (maximum or minimum) at

`\displaystyle t=-(b)/(2a)`

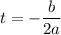
If a>0, it's a maximum, otherwise it's a minimum

. Since a=-16, we'll get a maximum.

Computing the value of t to make the height be maximum

`\displaystyle t=-(15)/(2(-16))=0.47\ sec`

The basketball reaches its maximum height at t=0.47 seconds

Part 4

The maximum height can be computed by using the function of h evaluated in t=0.47 sec

`h(t)=-16t^2+15t+6.5`

`h_m=-16(0.47)^2+15* 0.47+6.5`

`h_m=3.52\ feet`

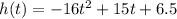
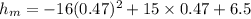
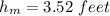
The maximum height of the ball is 3.52 feet