Answer:
80°
Explanation:
We have redrawn the figure with nomenclature.
Given,
∠C = 45°
∠D = 55°
We have to find the value of x.
Solution,
In ΔCDE
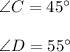
Now according to angle sum property;
Sum of all the angles of a triangle is equal to 180°.
framing in equation form, we get;
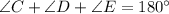
On substituting the given values, we get;
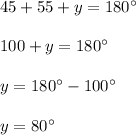
Now In Δ AEB and Δ CED
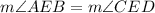 ⇒ (Vertically opposite angles.)
⇒ (Vertically opposite angles.)
Now
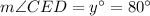
So
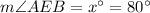
Hence
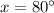 .
.