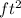Question

A sector of a circle has a central angle of 145°. Find the area of the sector if the radius of the circle is 4 ft. (Round your answer to one decimal place.)

Answer 1

20.2 square feet

Explanation:

A sector of a circle is just a piece of the circle, like a piece of a pie.

A sector of a circle that has a central angle of 145 degrees would look like the attached photo.

So to find the area of this sector, you would need to find a fraction, or a part, of the area of the whole circle, right?

Now we know that the radius of the circle 4 feet. The formula for calculating the area of a circle is A = π
`r^2`.

We can plug in r = 4 into the formula, giving us A = 16π, because
`4^2 = 16`.

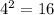So 16π is the area of the entire circle.

To find the area of the sector, we need to figure out what fraction of the circle is shaded in.

If we know a whole circle is 360 degrees, we can divide 145 degrees by 360 degrees to find the fraction of the circle that is shaded in. 145/360 ≈ 0.4027777.

0.4027777 is a little less than 0.5, or one half, and if we look at our diagram, this is the right fraction.

Now, we can multiply the area of the circle by this fraction to find the area of the sector.

`A_(C)` * 0.4027777 =
`A_(S)`

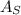
16π * 0.4027777 =
`A_(S)`

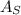
16(3.14) * 0.4027777 ≈ 20.2
`ft^2`