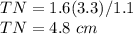Question

(answer questions about the picture above)

1. For ∆TRI the following facts are given:
Segment AN || Segment RI
AN=6cm
RI=8cm
TA=3.3
NI=1.6

Use any or all of these facts to answer the following:

a) Assume ∆TRI was dilated to become the image ∆TAN. Is the dilation and expansion or a contraction?

b) What is the scale factor?

c) Calculate AR. Show your work.

d) Use the Side-Splitting Theorem to find TN.

Answer 1

Part a) The dilation is a contraction

Part b) The scale factor is 0.75

Part c)
`AR=1.1\ cm`

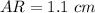
Part d)
`TN=4.8\ cm`

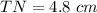
Explanation:

Part a) Assume ∆TRI was dilated to become the image ∆TAN. Is the dilation an expansion or a contraction?

We have that

The pre-image is the triangle TRI (original figure)

The image is the triangle TAN (dilated figure)

we know that

If the image is smaller than the pre-image then the dilation is a contraction or reduction

If the image is greater than the pre-image then the dilation is a expansion or enlargement

The triangle TAN is smaller than triangle TRI

so

the image is smaller than the pre-image

therefore

The dilation is a contraction

Part b) What is the scale factor?

we know that

A dilation is a non-rigid transformation that produces similar figures

If two figures are similar, then the ratio of its corresponding sides is proportional and this ratio is called the scale factor

In this problem

triangle TAN ~ triangle TRI

Let

z ----> the scale factor

`z=(AN)/(RI)`

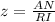
AN and RI are corresponding sides

substitute the given values

`z=(6)/(8)=0.75`

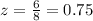
Part c) Calculate AR. Show your work

Remember that the ratio of its corresponding sides is proportional and is equal to the scale factor

so

`(TA)/(TR)=z`

substitute the given values

`(3.3)/(TR)=0.75`

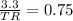
Solve for TR

`TR=3.3/0.75\\TR=4.4\ cm`

Find the length of AR

we know that

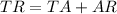`TR=TA+AR` ----> by segment addition postulate

substitute the given values

`4.4=3.3+AR\\AR=4.4-3.3=1.1\ cm`

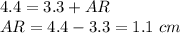
Part d) Use the Side-Splitting Theorem to find TN.

we know that

The side splitter theorem states that if a line is parallel to a side of a triangle and the line intersects the other two sides, then this line divides those two sides proportionally

Applying the Side-Splitting Theorem

`(TN)/(NI)=(TA)/(AR)`

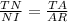
substitute the given values

`(TN)/(1.6)=(3.3)/(1.1)`

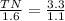
solve for TN

`TN=1.6(3.3)/1.1\\TN=4.8\ cm`