Answer:
AC = 11.518 cm
Explanation:
Given ,
BC = 4 cm
∠ b = ∠ c = x ( say )
∠ a = 20°
AC = ?
From the given data it is known that Δ ABC is isosceles triangle and we know that sum of angles of a triangle is 180° .
⇒ ∠ a + ∠ b + ∠ c = 180°
⇒ 20° + x + x = 180°
⇒ 2x = 160°
⇒ x = 80 °
∴ ∠ b = ∠ c = 80°
Now by applying sine rule,
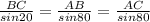
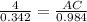 ( sin 20 = 0.342 & sin 80 = 0.984 )
( sin 20 = 0.342 & sin 80 = 0.984 )
AC = 11.518 cm