Question

My aim is to minimise function 3A + 5B Where A is an island which needs to be connected to a point B (say hotel) by a cable. We need to minimise the cost. Price of a cable going under the water is 3 dollars and underground 5 dollars. The distance between A and shoreline is 2 as same as the distance between B and shoreline. The distance between A and B in a straight shoreline line is 7. I can't find the right constraints to my problem. I tried to divide the shoreline into tho segments x and 7-x. Which creates two triangles with sides 2, 7-x and 2, x. Is it a good idea? A, B >= 0 but how connect other values to make equations? Thank you

Answer 1

Lay the cable so it touches the shore 1.5 km from A, and 5.5 km from B.

Explanation:

Your description is pretty murky, but if it is similar to other such problems, then you are off to a good start. (I think). I assume you meant something like this:

A is an island 2 km off shore, and B is 7 km away from the point on shore closest to A. Laying cable costs $5/km underwater, and $3/km underground. Find the minimum cost of connecting A to B by cable. Why did I switch the costs? Because if underwater is cheaper, then just lay the cable straight from A to B!

To find The distance x from A that minimizes the cost, you have

underwater distance:
`√(4+x^2)`

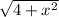
underground distance: 7-x

So, the cost

c(x) = 5
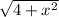`√(4+x^2)` + 3(7-x)

To minimize the cost, you need to find where dc/dx = 0

dc/dx = 5x/
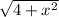`√(4+x^2)` - 3

dc/dx=0 when

5x = 3
`√(4+x^2)`

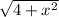
25x^2 = 9(4+x^2)

x = 3/2

c(3/2) = 29

So, the point 1.5 km from A makes the cost minimum.