Question

The volume of a right rectangular solid is 1536 ft3. Find the height of the solid, if the length is 2 times the width, and the height is twice the perimeter of the base.

Answer 1

Height: 48 feet.

Explanation:

Let W represent width of the rectangular solid.

We have been given that length is 2 times the width, so the length of the solid would be
`2W`.

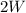We know that the perimeter of base of the cuboid is equal to 2 times sum of length and width.

We are also told that the height is twice the perimeter of the base.

`H=2(2L+2W)`

`H=2(2*2W+2W)`

`H=2(4W+2W)=2*6W=12W`

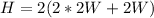
We know that volume of cuboid is equal to length times width time Height.

We have been given that volume of a right rectangular solid is 1536
`\text{ft}^3`. We can represent our given information as:

`L\cdot W\cdot H=1536`

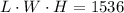
Upon replacing length and height in terms of width, we will get:

`2W\cdot W\cdot 12W=1536`

`24W^3=1536`

`(24W^3)/(24)=(1536)/(24)`

`W^3=64`

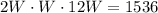
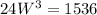
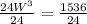
Take cube root of both sides:

`\sqrt[3]{W^3}=\sqrt[3]{64}`

`W=4`

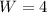
Therefore, the width of the solid is 4 feet.

Let us find Height of the solid as:

`H=12W\Rightarrow12(4)=48`

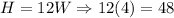
Therefore, the height of the rectangular solid is 48 feet.