Question

If the radius of a circle is 5 units, in square units what is the sector area given m(arc)=142

Answer 1

The correct option is 30.6

Therefore,

Area of Sector is 30.6 units².

Explanation:

Given:

Central angle = θ = 142°

Radius = r = 5 units

pi = 3.14

To Find:

Area of Sector = ?

Solution:

If the θ measured in degree then the Area of Sector is given as

`\textrm{Area of Sector}=(\theta)/(360\°)* \pi r^(2)`

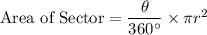
Where r = radius, θ = Central angle

On substituting the values we get

`\textrm{Area of Sector}=(142)/(360\°)* \pi (5)^(2)`

`\textrm{Area of Sector}=0.39* 3.14* (5)^(2)`

`\textrm{Area of Sector}=30.615\ units^(2)`

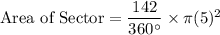
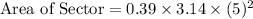
Therefore,

Area of Sector is 30.6 units².