The given question is wrong.
Question:
What is the solution set to the inequality (4x – 3) (2x – 1) ≥ 0?
(A)
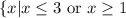
(B)
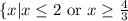
(C)
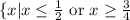
(D)

Answer:
The solution set to the given inequality is
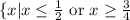 .
.
Solution:
Given expression is (4x – 3) (2x – 1) ≥ 0.
Let us take the expression is equal to zero.
(4x – 3) (2x – 1) = 0
By quadratic factor, If AB = 0, then A = 0 or B = 0.
(4x – 3) = 0 or (2x – 1) = 0
Let us take the first factor equal to zero.
⇒ 4x – 3 = 0
⇒ 4x = 3
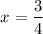
Now, take the second factor equal to zero.
⇒ 2x – 1 = 0
⇒ 2x = 1

So,
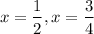 .
.
Now, write it in the inequality to make the statement true.
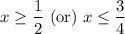
Option C is the correct answer.
The solution set to the given inequality is
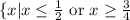 .
.