Question

A 0.90- kg mass attached to a vertical spring of force constant 170 N/m oscillates with a maximum speed of 0.20 m/s . Find the following quantities related to the motion of the mass.

Find the period.

Find the amplitude.

Find the maximum magnitude of the acceleration.
Express your answer using two significant figures.

Answer 1

Step-by-step explanation:

Given that,

The mass of the object, m = 0.9 kg

Force constant, k = 170 N/m

Maximum speed of the object, v = 0.2 m/s

Solution,

(a) The angular frequency of the object is given by :

`\omega=\sqrt{(k)/(m)}`

`\omega=\sqrt{(170)/(0.9)}`

`\omega=13.74\ rad/s`

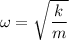
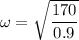
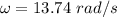
The time period is given by :

`T=(2\pi)/(\omega)`

`T=(2\pi)/(13.74)`

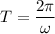
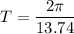
T = 0.45 seconds

(b) The maximum velocity of the object in shm is given by :

`v=A\omega`

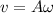
Amplitude,

`A=(v)/(\omega)`

`A=(0.2)/(13.74)`

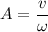
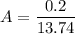
A = 0.0145 m

(c) The maximum acceleration of the object is given by :

`a=\omega^2A`

`a=(13.74)^2* 0.0145`

`a=2.73\ m/s^2`

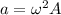
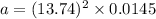
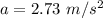
Therefore, this is the required solution.