Question

. An expedition in the arctic sea to study the e ect of climate change on deep-ocean ecosystemrequires precise measurement of temperature and pressure variations at the probe location. Theprobe is housed in a 40 cm diameter spherical shell. The emissivity of the shell surface is 0.85.Because of the precision instruments, it is important that the temperature of the shell remainsconstant at 10C. To achieve this, you need to design a heater that will be placed inside the shell.Ignore the e ect of solar irradiation (night condition).

Answer 1

The complete question contains 2 parts such that

part a: Where the probe is submerged in water. In this case the wattage of heater is 90.47 W

part b: Where the probe is on a vessel. In this case the wattage of heater is So 121.34 W

Step-by-step explanation:

Part a

For the first part when it is assumed that the probe is submerged in the water. In this case the heat loss is only due to the convective heat transfer which is given as

`Q=h * A * (T_(body)-T_(surr))`

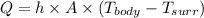
Here

• Q is the heat loss which is to be calculated

• A is the area of the body which is given as
  `4 \pi r^2 \\`. It is calculated as

`A=4 \pi r^2 \\A=4 * 3.14 * (0.2)^2 \\A=0.5026 m^2`

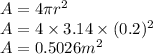
• Tbody is 10 C
• Tsurr is 0C
• h is the convection coefficient of water which is 18 W/m^2K

`Q=h * A * (T_(body)-T_(surr))\\Q=18 * 0.5026 * (10-0)\\Q=90.47 W\\`

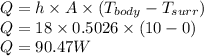
So the wattage of heater is 90.47 W

Part b

Now when the probe is above sea water now, the losses are both because of convection and radiation now the loss is given as

`Q_(con)=h_(air) * A * (T_(body)-T_(air))`

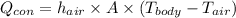
Here

• Q_con is the heat loss due to convection which is to be calculated

• A is the area of the body which is given as 0.5026 m^2

• Tbody is 10 C
• Tair is -10C
• h is the convection coefficient of water which is 10 W/m^2K

`Q_(con)=h_(air) * A * (T_(body)-T_(air))\\Q_(con)=10 * 0.5026 * (10+10)\\Q_(con)=100.52 Watts`

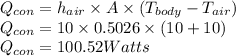
Radiation loss is given as

`Q_(rad)=E_(emission)-E_(radiation)\\Q_(rad)=\epsilon A \tau (T_(body)^4-T_(sky)^4)\\`

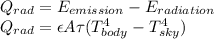
Here

• Q_rad is the heat loss due to radiation which is to be calculated

• A is the area of the body which is given as 0.5026 m^2

• Tbody is 10+273=283K
• Tsky is 0+273=273K
• ε is the emissivity of the shell which is 0.85

• τ is the coefficient which is
  `5.67 * 10^(-8)`

`Q_(rad)=E_(emission)-E_(radiation)\\Q_(rad)=\epsilon A \tau (T_(body)^4-T_(sky)^4)\\Q_(rad)=0.85 * 0.5026 * 5.67 * 10^(-8) ((283)^4-(273)^4)\\Q_(rad)=20.823 Watts`

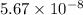
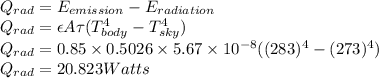
So the total value of heat loss is

`Q_(total)=Q_(convective)+Q_(radiation)\\Q_(total)=100.52+20.823 W\\Q_(total)=121.341 W`

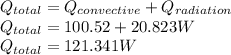
So the wattage of heater is 121.34 W