Question

A ball is thrown into the air with an upward velocity of 100 ft/s. Its height after T seconds is given by the function f (x) = -16t^2 + 64t + 960. How many seconds did it take for the ball to reach its maximum height?

Answer 1

The ball will reach its maximum height at 2 seconds after being launched

Explanation:

Vertical Launch

The height of a ball thrown into the air is given by

`f (t) = -16t^2 + 64t + 960`

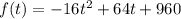
Where t is the time in seconds after the ball was released. We want to find the time when the ball reaches a maximum point, i.e. the time that makes
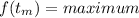`f(t_m) = maximum`. The equation of f(t) is a parabola which is known for having a vertex located at the point

`\displaystyle t=-(b)/(2a)`

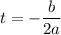
where a and b are given by the general formula of the parabola

`f(t)=at^2+bt+c`

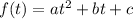
For our ball, the time needed to reach the maximum height is

`\displaystyle t=-(64)/(2(-16))=2\ sec`

The ball will reach its maximum height at 2 seconds after being launched