Question

Urn 1 contains two white balls and one black ball, while urn 2 contains one whiteball and ve black balls. One ball is drawn at random from urn 1 and placed in urn2. A ball is then drawn from urn 2. It happens to be white. What is the probabilitythat the transferred ball was white?

Answer 1

4/5 is the probability of white ball from urn 2

Explanation:

Correct statement of the question is ;

Urn 1 contains two white balls and one black ball, while urn 2 contains one white bait and five black balls. One ball is drawn at random from urn 1 and placed in urn 2. A ball is then drawn from urn 2. It happens to be white. What is the probability that the transferred ball was white?

We solve it ;

Probability of taking out balls from urn 1

a) for white ball

`P(w_(1) )=(2)/(3)`

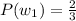
b) for balck ball

`P(b_(1) )= (1)/(3)`

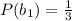
If one ball is taken from urn 1 and put in urn 2 (which readily contains one white and five black balls)

Probability of taking out balls from urn 2

a) for white ball

`P(w_(2) )=P((w_(2) )/(w_(1) ) ).P(w_(1) )+P((w_(2) )/(b_(1) ) ).P(b_(1) )`

`=(2)/(7) . (2)/(3) + (1)/(7). (1)/(3) =(5)/(21)`

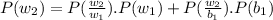
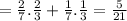
Then the probability that white ball was transferred from urn 1 to urn 2 is;

`P((white ball transfer )/(w_(2) ) )= (P((w_(2) )/(w_(1) ) ).P(w_(2) ))/(P(w_(2)) )`

`=( (2)/(7).(2)/(3) )/((5)/(21) )`

`=(4)/(5)`

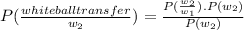
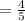
So, the probability that white ball is drawn from urn 2 is 4/5