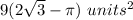Question

Write an expression in simplest radical form INTERMS OF PI that represents the difference between Leilani's approximated área and Desmond's actual area

Please show the steps

Answer 1

`9(2√(3)-\pi)\ units^2`

Explanation:

step 1

Find Leilani's approximated área

we know that

The approximate area of the circle is approximately the area of the six equilateral triangles

The formula to calculate the length side of a regular hexagon given the radius of a inscribed circle is equal to

`a=(2r√(3))/(3)`

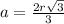
where

a is the length side of a regular hexagon

r is the radius of the inscribed circle

we have

`r=3\ units`

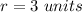
substitute

`a=(2(3)√(3))/(3)`

`a=2√(3)\ units`

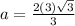
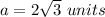
Find the area of six equilateral triangles

`A=6[(1)/(2)(r)(a)]`

simplify

`A=3(r)(a)`

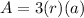
we have

`r=3\ units\\a=2√(3)\ units`

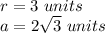
substitute

`A=3(3)(2√(3))\\A=18√(3)\ units^2`

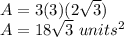
step 2

Find Desmond's actual area

we know that

The area of a circle is equal to

`A=\pi r^(2)`

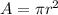
we have

`r=3\ units`

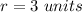
substitute

`A=\pi (3)^(2)`

`A=9\pi\ units^2`

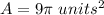
step 3

Find the difference between Leilani's approximated área and Desmond's actual area

`(18√(3)-9\pi)\ units^2`

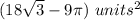
simplify

`9(2√(3)-\pi)\ units^2`